Search Results
Companies
Eta Gas
Eta GaS will act as a catalysator for innovation to efficiency increasing in Anaerobic Digestion con.....
Sirajganj Eco-Energy Limited
Sirajganj utilizes municipal and commercial waste as recycling and fuel production services. The.....
Pesud Abadi Mahakam
Pesud Abadi Mahakam is an International Trading Company that focuses on Commodities Trading across t.....
ZELT RENEWABLE ENERGY
Zelt Solar Electricals is a solar retail business focusing in shipping, delivery, and installat.....
North Power Company
NPC offers design, selling, and delivery of solar technology. Also, this company provides solar ener.....
MEGA SOLAR SOLUTIONS
This company has been working since 2004 in the Solar energy sector, especially in Solar Inverters,.....
Soguard hydrogen UK
Soguard-hydrogen-Uk specialises in Hydrogen technology, production and installation equipment. This.....
Biomass Research
Biomass Research is a dynamic research and consulting firm devoted to the development, analysis and.....
GenH2 Discover Hydrogen
Developing systems using patented technologies and licenses, GenH2 is building efficient manufa.....
Publications
Optimizing ethanol and bioelec...
In sugarcane biorefineries, the lignocellulosic portion of the sugarcane biomass (i.e. bagasse and c.....
Power generation from sugarcan...
This paper discusses the complementarity between hydroelectricity and surplus electricity from sugar.....
Net energy balance of molasses...
This paper evaluates life cycle energy analysis of molasses based ethanol (MOE) in Nepal. Net energy.....
Greenhouse gas balances of mol...
This paper evaluates life cycle greenhouse gas (GHG) balances in production and use of molasses-base.....
Energy and GHG balances of eth...
This study analyses the sustainability of fuel ethanol production from cane molasses in Indonesia. L.....
Accounting greenhouse gas emis...
This study discusses four European and American regulatory schemes designed for accounting lifecycle.....
Land allocation to meet sector...
Land is a scarce resource affecting the implementation of many sectoral policies. In Indonesia, the.....
Cost competitiveness of palm o...
This study investigates opportunities to improve the cost competitiveness of the palm oil biodi.....
Well-to-Wheel analysis of foss...
This study estimates Well-to-Wheel (WTW) fossil energy use and greenhouse gas (GHG) emissi.....
Ethanol production and fuel su...
This paper explores the potential for ethanol production and fuel substitution in Nepal based on est.....
Scenarios for bioethanol produ...
This study investigates the potential of bioethanol production and fossil fuel substitutio.....
Evaluating the palm oil demand...
This paper investigates the development of domestic and international demand for Indonesian palm oil.....
Opportunities to optimize the...
Significant amounts of biomass residues were generated in Indonesia. While untreated, residues emit.....
Opportunities for bioenergy in...
Security of energy supply, promotion of the bio-economy, nutrient recycling, and innovation are prio.....
The influence of passenger loa...
This study analyses the influence of passenger load, driving cycle, fuel price and four different ty.....
Policies and modeling of energ...
To mitigate carbon dioxide emissions, the European Union (EU) and many countries around the world ha.....
Sugarcane Biofuel Production i...
Indonesia has a long history of sugar production and a significant potential to enhance both sugar a.....
Mapping Bioenergy Supply and D...
Bioenergy can play an important role in achieving the agreed United Nations Sustainable Development.....
Conditions for sugarcane biofu...
Indonesia has a long history of sugar production and a significant potential to enhance both sugar a.....
Sustainable Bioenergy Developm...
Indonesia is the largest country in Southeast Asia. With a challenging geography, growing population.....
The role of ethanol from suga...
Global concerns related to the sustainability of energy systems and climate change, as well as incre.....
Bio-diesel from jatropha: from...
Rapidly decreasing fossil-fuel reserves of the world have led to an intensive search for alternative.....
Biomethane production with ref...
Escalating energy costs and energy shortages in recent years have become problems ofnational signifi.....
Water4Crops-EU: Report on the...
Work Package 1 focuses on valorization, treatment and reuse of agrofood industry wastewaters. Two ty.....
Strategic Research Agenda on b...
Our fast growing and developing world is facing problems such as environmental deterioration, biodiv.....
An Overview of Carbon and Nano...
Bioelectrochemical systems (BESs) have gained much attention in the field of energy sources due to t.....
Editorial: Microbial Synthesis...
The ongoing climate crisis, mainly caused by the emission of greenhouse gases (GHGs), gives rise to.....
Techno-productive evaluation o...
Acid mine drainage (AMD) presents severe ecological pollution challenges because of its extreme acid.....
Advanced routes of biological...
Changes in the environment due to multiple factors, such as combustion of fossil fuels, heating, tra.....
Electrosynthesis of Biobased C...
The current climate awareness coupled with increased focus on renewable energy and biobased chemical.....
Microbial Electrosynthesis: A...
There has been a considerable increment in the atmospheric CO2 concentration, which has majorly.....
Prime Techniques for Pre- and...
Several pre-treatment approaches have been explored to enhance the anaerobic fermentation kinetics a.....
Efficiency of Graphene-Based F...
Although forward osmosis (FO) has escalating prospective applications, several key challenges are st.....
Perspectives of Environmental...
Microbes are the integral parts of the nature and played an important role in natural recycling of m.....
Towards highly efficient elect...
An increase in atmospheric CO2 concentration is directly associated with the rising concerns of.....
Moving towards practical appli...
Sanitation is the basic quality index of life and proper sanitation practices play a vital role in m.....
Microbial Electrochemical Tech...
This book encompasses the most updated and recent account of research and implementation of Microbia.....
Microbial electrosynthesis fea...
An enrichment methodology was developed for a homoacetogenic biocathode that is able to function at.....
Development and life cycle ass...
Bioelectrochemical systems like microbial fuel cells (MFCs) are quaint systems known to metamorphose.....
Circular economy aspects of li...
Lignin is the second most abundant polymer, which comprises15-30% (dry weight) of total lignocellulo.....
Chronoamperometry and linear s...
Anode performance in microbial fuel cell (MFC) is usually examined by monitoring anode potentials in.....
Key issues in life cycle asses...
Progressive depletion of conventional fossil fuels with increasing energy consumption.....
Electro-Fermentation—Microbial...
Electro-fermentation (EF) merges industrial fermentation with electrochemistry toward a new biotechn.....
Integrated Bioelectrochemical...
Energy and water are intrinsically linked, as all energy sources need water for their production pro.....
Resource recovery from wastes...
Recent scientific and technological advancements in bioelectrochemical system (BES) research have op.....
Material–Microbe Interfaces fo...
Sustainable production of solar-based chemicals is possible by mimicking the natural photosynthetic.....
Reactor Design for Bioelectroc...
Bioelectrochemical systems (BES) are novel hybrid systems which are designed to generate renewable e.....
Biological Electricity Product...
Attributed to their multifaceted abilities, microorganisms have been constantly explored for several.....
Bioprocesses for Waste and Was...
Microbial metabolism of pollutants is the key process involved in energy generation along with remed.....
Sulfide as an alternative elec...
The objective of this study was to investigate the power generation in a dual-chamber microbial fuel.....
Microbial recycling cells: fir...
The aim of this work were to study terracotta-based porous air-water separators (4 mm thickness) in.....
Possibilities for the biologic...
In the course of dark fermentative hydrogen production, a complex gaseous mixture with significant q.....
Microbial electrochemical tech...
Carbon dioxide (CO2) valorization for the production of different commodity chemicals is a highly de.....
A Comparison of Life Cycle Ass...
The intensive increase of biofuel demand has pushed the researchers to find a sustainable biofuel pr.....
Cathodes for microbial fuel ce...
Increase in human activities across the globe has put forward several challenges for future generati.....
Innovative graphene microbial...
Supplying clean water to fulfill human requirements is one of this century’s priorities. Globa.....
Electrode material properties...
The electrode material is one of the key components of a bioelectrochemical system (BES), serving as.....
Bioelectrofuel Synthesis by Na...
Recent bioinspired efforts of designing novel nanoenzyme-based electrocatalysts are driven by the ur.....
Utilization of residual organi...
Labaneh whey (LW) that is rich in residual organics was evaluated for bioelectricity generation usin.....
Towards the development of a b...
India has emerged as a key player with a high potential to develop a biomass and biobased economy du.....
Bioelectrochemical Systems (BE...
Bioelectrochemical systems (BES) have been employed for various applications in recent years includi.....
Optimization of electrochemica...
This study focuses on the effect of operational and physiochemical factors on a stable sulfate reduc.....
Fabrication of a carbon paper/...
The use of platinum (Pt) catalysts in air cathode for microbial fuel cells (MFCs) is expensive and i.....
Sustainable utilization of cro...
Modernization in the crop cultivation and development of high yielding varieties resulted in increas.....
Enhancement of bio-ethanol pro...
The present study intended to enhance the bioethanol productionpotential of wheat straw by redu.....
Microalgae at niches of bioele...
Bioelectrochemical system represents a novel technology where the microbial catalytic reaction occur.....
Valorization of agricultural w...
Environmental deterioration and the need for energy security are intrinsic problems linked with the.....
Gas Diffusion Electrodes Manuf...
One of the most intriguing renewable energy production methods being explored currently is electrica.....
Bioelectrochemical synthesis o...
Chain elongation is one of the common anaerobic fermentation processes in which bacteria convert eth.....
Evaluation and enhanced operat...
The present study evaluates the performance of air-cathode microbial fuel cells (MFCs) under alterna.....
Shift to continuous operation...
Microbial fuel cells (MFCs) which are operated in continuous mode are more suitable for practical ap.....
Trends and sustainability crit...
Anthropogenic greenhouse gas (GHG) emissions are changing our Earth’s climate very rapidly and.....
Current Trends in Enzymatic El...
Enzymatic electrosynthesis offers a novel approach to the production of chemicals through CO2 s.....
Treatment of rayon grade pulp...
The Rayon grade pulp (RGP) drain effluent of pulp and paper mill was studied to find out pollutant l.....
Influence of headspace composi...
Mixed culture of sulphate reducing bacteria named TERI-MS-003 was used for development of biocathode.....
Assessment of Expanded Polysty...
Separators are considered as an important component in microbial fuel cells (MFCs) to facilitate ion.....
Long-term open circuit microbi...
Microbial electrosynthesis (MES) can potentially provide a mean for storing renewable energy&nb.....
Microbial electrosynthesis fro...
Recycling CO2 into organic products through microbial electrosynthesis (MES) is attractive from.....
Integrated Photobioelectrochem...
Recent breakthroughs have reinvigorated the century-old research domain of artificial photosynt.....
A comprehensive impedance jour...
The aim of the present work was to characterize the impedance response of an air-cathode M.....
Solvents and Supporting Electr...
Different electrolytes applied in the aqueous electrocatalytic CO2 reduction reaction (CO2RR) c.....
Microbial Fuel Cells: Electrod...
Microbial fuel cell (MFC) is an electrochemical device in which electroactive bacteria are used.....
Impact of Dissolved Carbon Dio...
The reduction of carbon dioxide (CO2) released from industry can help to reduce the emissions of gre.....
Performance and inorganic foul...
A submergible 255 L prototype MFC module was operated under practical conditions with municipal wast.....
In situ acetate separation in...
Bioelectrochemical reduction of carbon dioxide (CO2) to multi-carbon organic compounds particularly.....
Suppressing methanogens and en...
Suppression of methanogens is considered as one of the main challenges in achieving the practical ap.....
Bioelectrochemical Conversion...
The recent concept of microbial electrosynthesis (MES) has evolved as an electricity-driven producti.....
Catalytic performance of nano-...
Finite resources of the world's fossil fuel give rise to the irresistible urge to explore altern.....
Electro-biocatalytic conversio...
Impact of gas diffusion electrodes (GDEs) was evaluated in enhancing the CO2bio-availability for its.....
Effect of the electric supply...
Microbial electrosynthesis (MES) technology relies on the direct use of electrons to conve.....
Microbial electrosynthesis (ME...
Microbial electrosynthesis (MES) allow CO2 capture and utilization for the electricity-driven&n.....
Development of a novel fungal...
In India, cane molasses–based distilleries are major production centers of ethanol. These indu.....
In-situ biofilm removal from a...
One challenge in using microbial fuel cells (MFCs) for wastewater treatment is t.....
Assisting cultivation of photo...
Spirulina was cultivated in cathodic compartments of photo-microbial fuel cells (P-MFC). Anodic.....
Bio-analytical Applications of...
Globally, sustainable provision of high‐quality safe water is a major challenge of the 21st century......
Potential biovalorization tech...
The industrial process of olive oil extraction produces huge amounts of wastes that have great negat.....
Recent advances in industrial...
In light of the energy transition, electrochemical CO2 reduction (CO2R) has commonly been postu.....
Dual‐Function Electrocatalytic...
Dual‐function electrocatalytic and macroporous hollow‐fiber cathodes are recently proposed as promis.....
Dual gas diffusion cathode des...
Upscaling microbial fuel cells (MFCs) to make them energy‐competitive systems requires a systematic.....
Concentration of fungal lignin...
Extracellular ligninolytic enzymes secreted by seven different fungi grown under solid-state ferment.....
Identification, ligninolytic e...
Two fungal strains producing ligninolytic enzymes and having the potential to decolorize distillery.....
Development of gas diffusion e...
This study reports the development and evaluation of gas diffusion electrodes (GDEs) for application.....
Anode and cathode materials ch...
Microbial fuel cells (MFCs) are novel bioelectrochemical devices for spontaneous conversion of bioma.....
Electro-stimulated microbial f...
Interplay of charge between bacteria and electrode has led to emergence of bioelectrochemical system.....
Evaluating a multi-panel air c...
To scale up microbial fuel cells (MFCs), larger cathodes need to be developed that can use air direc.....
Key issues to consider in micr...
All nations have been confronted with the energy crisis due to depletion of finite fossil fuels rese.....
Agriculture biomass in India:...
The growing bioeconomy sector aims to reduce the amount of waste generated and to promote the unavoi.....
Continuous mode operation of m...
Three microbial fuel cells (MFC) with dual gas diffusion cathode design were operated individually i.....
Biohydrogen Production from Li...
Among the various renewable energy sources, biohydrogen is gaining a lot of traction as it has very.....
Life cycle assessment of renew...
Governments are setting challenging targets to increase the production of energy and transport fuel.....
An enriched electroactive homo...
In the direction of generating value added chemicals from carbon dioxide (CO2) reduction through mic.....
Agriculture biomass in India:...
Biomass residues or wastes generated in the agricultural sector represent a source of potentially su.....
Bioelectroremediation of perch...
Fresh water is a fundamental source for humans, hence the recent shrinkage in freshwater and increas.....
Characterization and compariso...
Bioelectricity production from microbial fuel cell (MFC), fed with synthetic wastewater can achieve.....
Integrated conversion of food...
In this study, domestic wastewater was given a second life as dilution medium for concentrated organ.....
Bioelectro-catalytic valorizat...
Biovalorization of dark fermentation effluent (DFE) in a microbial fuel cell(MFC) was.....
Cultivation of oyster mushroom...
Molasses-based distilleries produce large quantities of dark coloured effluent, which is a.....
Nanotechnology to rescue the b...
An electrically active bacterium transports its metabolically generated electrons to insoluble subst.....
Key issues in estimating energ...
The increasing demand for biofuels has encouraged the researchers and policy makers worldwide to fin.....
Application of gas diffusion b...
Microbial catalysis of carbon dioxide (CO2) reduction to multi-carbon compounds at the cathode is a.....
Applications of graphene in mi...
Since the initial emergence of two-dimensional graphene (Gr) nano-material, there has been a great i.....
The near-future integration of...
The combined negative effect of both fresh water shortage and energy depletion has encouraged the re.....
Enzymatic electrosynthesis of...
Bioelectrochemical system (BES) was operated using the enzyme formate dehydrogenase as catalyst at c.....
Enhanced production of lignino...
Selected isolates of fungi were grown on wheat straw and corncob in the presence of different moiste.....
Long-term operation of microbi...
In microbial electrosynthesis (MES), CO2 can be reduced preferably to multi-carbon chemicals by.....
Technological advances in CO2...
The global atmospheric warming due to increased emissions of carbon dioxide (CO2) has attracted grea.....
Techno-productive potential of...
The shortage of sustainable energy and the extensive environmental pollution along with the global w.....
Valorization of cereal based b...
The growth of the biobased economy will lead to an increase in new biorefinery activities. All biore.....
Biotransformation of carbon di...
Carbon dioxide (CO2) utilization/recycling for the production of chemicals and gaseous/liquid energy.....
Food and agricultural wastes a...
Bioelectrochemical systems (BESs) are one of the recent promising technologies developed for their m.....
Electro-Fermentation–Merging E...
Electro-fermentation (EF) merges traditional industrial fermentation with electrochemistry. An impos.....
A critical revisit of the key...
Many microorganisms have the innate capability to discharge and/or receive electrons to and from sol.....
A logical data representation...
Microbial electrosynthesis (MES) is a process that uses electricity as an energy source for driving.....
Internal resistance of microfl...
The efficiency of microbial fuel cells (MFCs) is affected by several factors such as activation over.....
Long‐Term Performance of Chemi...
Activated carbon (AC) is a low‐cost and effective catalyst for oxygen reduction in air cathodes of m.....
Carbon dioxide reduction by mi...
Carbon dioxide (CO2) reduction to multi-carbon compounds at the cathode using chemolithoautotrophs i.....
High strength wastewater treat...
Microbial fuel cells (MFCs) present a novel method for simultaneous bioelectricity generation and wa.....
Use of novel permeable membran...
In the existing microbial fuel cells (MFCs), the use of platinized electrodes and Nafion® a.....
An overview on emerging bioele...
Bioelectrochemical systems (BESs) are unique systems capable of converting chemical energy .....
The accurate use of impedance...
The present critical review aims to portray the principles and theoretical foundations that have bee.....
Waste Biorefineries: Enabling...
This paper aims to examine the potential of waste biorefineries in developing countries as a solutio.....
An introduction to the life cy...
Bioelectrochemical systems (BESs) are devices capable of converting organic waste fraction present i.....
Long-term performance of activ...
Activated carbon (AC) air-cathodes are inexpensive and useful alternatives to Pt-catalyzed electrode.....
Power generation using an acti...
An inexpensive activated carbon (AC) air cathode was developed as an alternative to a plat.....
Bioelectrochemical systems (BE...
Bioelectrochemical systems (BESs) are unique systems capable of converting the chemical energy of or.....
Key issues in life cycle asses...
Progressive depletion of conventional fossil fuels with increasing energy consumption and greenhouse.....
Recent advances in the use of...
The interest in the use of electroactive microorganisms for different applications by means of bioel.....
Biological approaches for trea...
Effluent originating from distilleries known as spent wash leads to extensive soil and water polluti.....
A review of the substrates use...
Microbial fuel cells (MFCs) have gained a lot of attention in recent years as a mode of converting o.....
Profitable biomethane producti...
In this study, a cost and time saving strategy for the recovery of biomethane from rice straw using.....
Enhanced bioelectrochemical tr...
Petroleum refinery wastewater (PRW) that contains recalcitrant components as the major portion of co.....
Modeling and optimization stra...
Considering the complexity associated with bioelectrochemical processes, the performance of a microb.....
Advances towards understanding...
The inhibition of the anaerobic digestion (AD) process, caused by long chain fatty acids (LCFAs), ha.....
Microbial electrosynthesis for...
Production of chemicals has significant influence on the emission of greenhouse gases (GHG) in parti.....
Bioelectrochemical Syntheses
Bioelectrosynthesis from CO2 offers the prospect to reuse CO2 emissions as a feedstock and.....
Review of Biogas Upgrading: Fu...
The growth potential of biogas upgrading is large. There are about 20.000 biogas plants in Europe to.....
Syngas production using straw...
Straw is one of the most available agriculture waste materials to be utilized as resource. Straw gas.....
Process Related Methane Loss f...
Biogas technology is one of the widely applied anaerobic digestion approaches to harvest methane fro.....
Coupling of microbial electros...
Anaerobic digestion (AD) has been widely applied bioprocess to produce the biogas for fuels from org.....
Conductive material engineered...
Biological syntrophy can be defined as a nutritional condition where various syntrophic microorganis.....
News & Blogs
Small-Scale Biogas Plant For C...
Biogas is a renewable energy source. It is produced from carbon-rich organic materials, such as agri.....
Renewable Energy Statistics 20...
Energy has been the prime driver of global economic development, industrialization and modernization.....
Biorefinery of Agricultural Re...
Biorefining is an efficient and innovative approach to sustainable biomass processing into a wide va.....
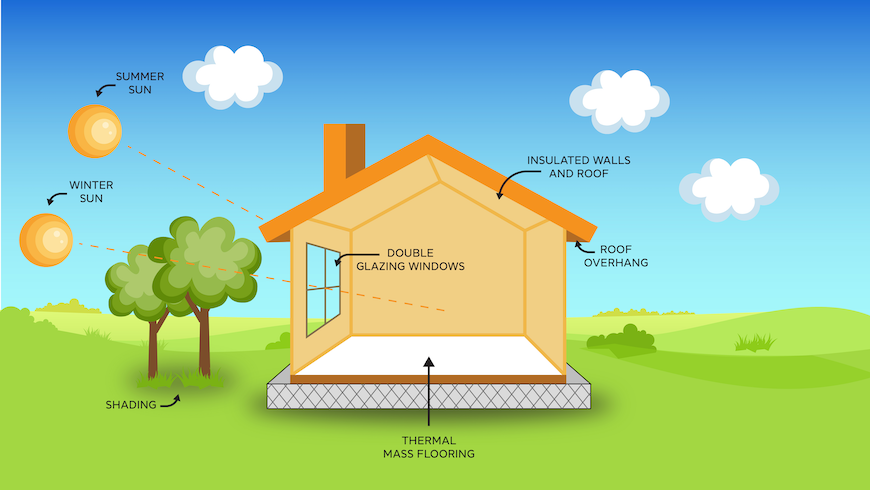
Thermal Mass Use for Heating a...
Thermal mass is the material’s ability to absorb and store heat energy before releasing it. It.....
Top Renewable Energy Career Pa...
In the last few years, the use of sustainable and renewable energy sources has been growing globally.....
How will Renewable Energy Cont...
The earth faces an undisputed global challenge of reducing fossil fuel consumption and increasing re.....
Solar Panel Cleaning: Is it wo...
Solar panel cleaning is an essential process to improve the efficiency of the panels. Solar panels c.....
The Complete Overview and Ulti...
Portable solar panels are small panels that can be carried out easily from one place to another. Tec.....
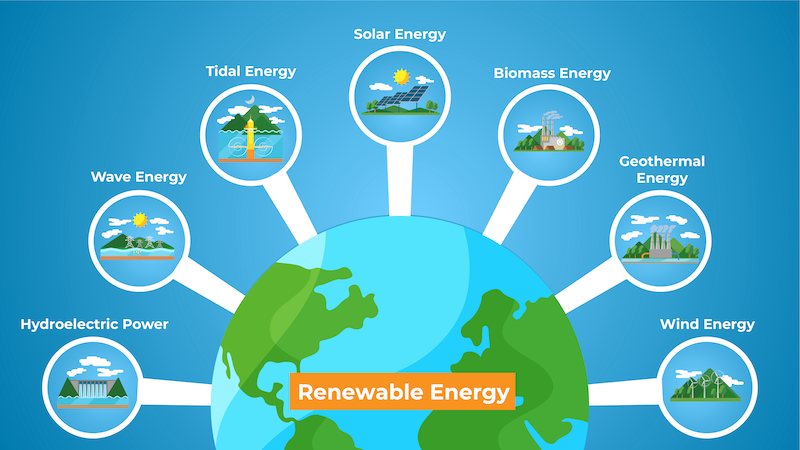
Renewable Energy: Sources and...
Overview: A global trend of searching for renewable energy as the primary energy source has becom.....
7 Tips for Using Natural Energ...
Making your home more energy efficient is something that many people are looking for. It's essen.....
Top 15 Renewable Energy Jobs o...
Renewable energy is a rapidly growing multidisciplinary area, including business, environmental scie.....
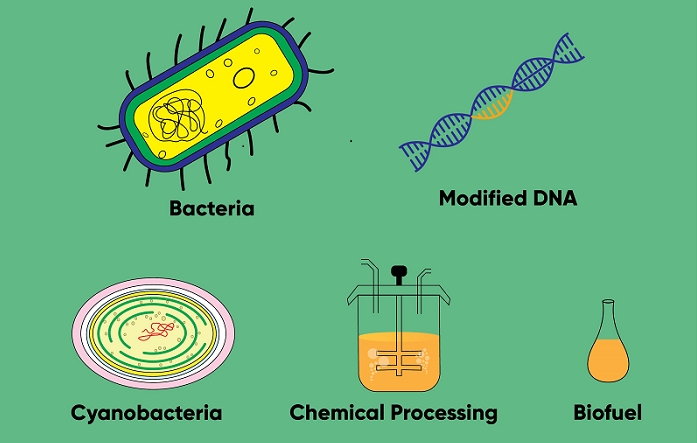
Genetic Engineering of microbi...
With the increasing concern and rising demand for clean and sustainable energy, biofuels are gaining.....
Nissan's Step towards Carbon N...
Nissan Motor Company has recently announced its plan to expand renewable energy generation at the Su.....
Genetic Modification of Plant...
Genetic modification, a genetic engineering process, is simply manipulating the gene to alter the ge.....
5 Reasons Why You Should Consi...
The energy demand is rising with the growth of the global population. People have been using renewab.....
Converting Plastic Wastes to N...
A new study conducted by the Swiss Federal Institute of Technology with the support of the Swiss Nat.....
Top 15 Renewable Energy Compan...
Sweden is a world-leading country when it comes to bioenergy. Currently, almost 54.6 percent of Swed.....
Top Energy Efficiency Examples...
We use energy every day for various purposes like cooking, transportation, lighting, heating, coolin.....
Apple Promises To Be 100 Perce...
On the occasion of Earth Day, April 22, 2021, multi-trillion tech giant company “Apple”.....
Facebook Becomes The Largest B...
On April 16, 2021, Mark Zuckerberg, Founder, and CEO of Facebook, announced that Facebook had become.....
Electric Vehicles: Everything...
The world is facing a rising concern of climate change and environmental degradation. To prevent cli.....
Top Renewable Energy Degrees t...
Climate change and environmental degradation are the major concerns of the present world. Various fa.....
The environmental implications...
One might think that only harmful energy sources like fossil fuels, oil, coal, and natural gas have.....
How Renewable Energy will tran...
The potentiality of humans to create innovative and technologically advancing resources with simply.....
List of Top 15 Renewable Energ...
The world’s 7th largest economy and Europe’s third-largest economy, France's renewab.....
Top 15 Renewable Energy Compan...
Denmark is one of the cleanest countries and when it comes to renewable energy, the country has beco.....
Top 15 Renewable Energy Compan...
New Zealand is one of the world’s most beautiful as well as peaceful countries. The country is.....
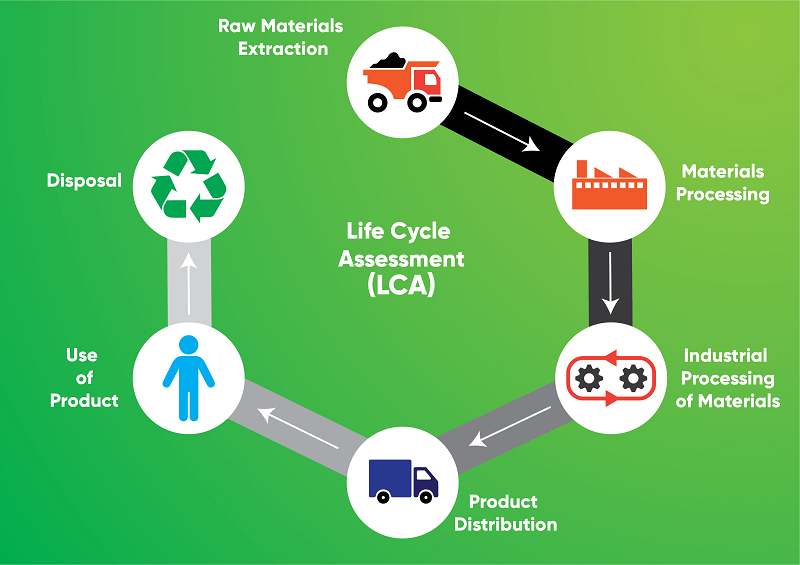
Life Cycle Assessment (LCA)- A...
Rapid industrialization around the globe has escalated environmental pollution, which has a severe i.....
Bamboo Biomass: A Potential Bi...
The rise in the global population has dramatically increased the production and use of non-biodegrad.....
Post-COVID-19 Urgency To Green...
The fossil fuels, such as oil, coal, and natural gas, are declining tremendously by precipitating th.....
Why is Bamboo the Sustainable...
The world is in the rapid pace of development with villages turning into towns, towns into cities, a.....
What Are The 17 Sustainable De...
The Sustainable Development Goals (SDGs) address global challenges we face and aims to achieve a bet.....
Bioenergy and Biofuels for a s...
Energy sources play a vital role to perpetuate modern life on earth. In the current global scenario,.....
A shift from conventional foss...
A question is raised about how our ancestors were and how we are today. The change seems obvio.....
Living Standard Of Rural Peopl...
A lot of factors determine how your lifestyle is dependent on where you are living. The living stand.....
Top 15 Renewable Energy Compan...
About 80% of the energy in the US comes from fossil fuels, however, there are American renewable ene.....
Top 15 Canadian Renewable Ener...
Canada is one of the leading countries in the production and innovation of renewable energy worldwid.....
Top 15 Companies affiliated to...
The United Kingdom is one of the oldest ruling civilizations in the world and they are also one of t.....
Butwal Solar Power Project Gen...
Butwal Solar Power Project is located in the Rupandehi District of Nepal. It has become Nepal's.....
Top 15 Companies Affiliated wi...
As much as the environment and surroundings of Australia are green, so is the renewable energy they.....
Australia built largest Solar...
With a cost of AUD$ 20 billion, photovoltaic panels spanning across 20,000 football fields, and a ca.....
15 Top Indian Solar Energy Co...
India is one of the biggest countries in the world and so is its plan for producing renewable energy.....
Big Oil Companies Are Rivaling...
As per the Consumer Report Survey, most American people won’t just prefer to choose their own.....
Top 15 Renewable Energy Compan...
Germany is one of the leading economies in the world and with Germany’s Energiewende (“e.....
Nepal’s Gautam Buddha Internat...
Gautam Buddha International Airport located in Bhairawa, Rupandehi is set to become the world’.....
List of Top 10 Iceland Renewab...
Currently, Iceland continues to be in the forefront position in the use of renewable energy. All ess.....
Top 15 Companies associated wi...
Norway is not just the land of Great Vikings but an island of renewable energy also. The country&rsq.....
Top 15 Renewable Energy Compan...
According to UN datum, India has a population of 1.380 Billion and is counted as the 7th largest cou.....
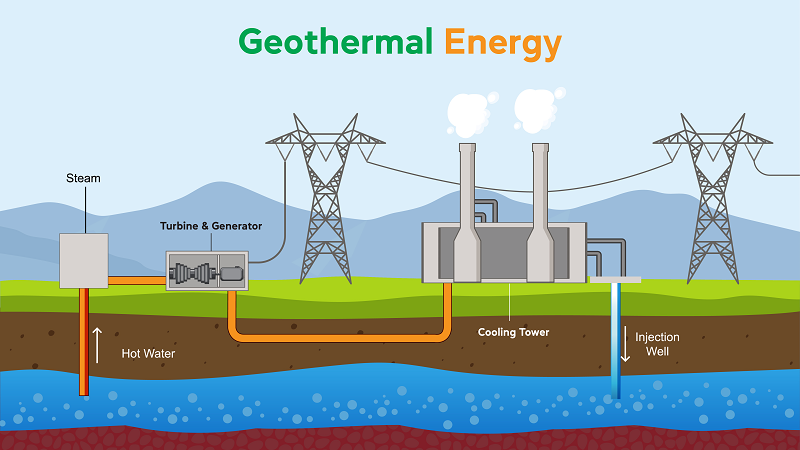
What Is Geothermal Energy? Typ...
Geothermal Energy needs an idle resource that holds the potential to meet the electricity and heatin.....
What is Solar Energy? Pros and...
Solar energy is the light and heat that appears from the sun and turns into electricity and heat ene.....
Biggest Solar Power Plant in N...
On Friday, Nepal’s Prime Minister KP Sharma Oli chaired the 44th meeting of the board in which.....
Top 15 Renewable Energy Compan...
Currently, Kenya leads the race to exploit renewable energy sources in Africa. Furthermore, renewabl.....
Products
Chelated micronutrients for AD
Chelated micronutrients - already the second generation. To make sure that never ever micronutrie.....
BEST SOLAR SOLUTION PROVIDER T...
We are pioneers in the field of Solar Power Plant & Panel Technology, we are manufacturers of In.....
Solar Panel
SolarUp is a solar panel installation company providing solar installations in Ontario. SolarUp&rsqu.....
10kwh ES-BOX6 rechargeable lit...
Model: ES-BOX6 Product specification: 51.2V100Ah Battery Voltage: 51.2V Battery Capac.....
10kwh ES-BOX5 battery backup f...
Model:ES-BOX5 Battery Type:LiFePO4 Energy:10240Wh Cycle life:6000-8000 times Rated Capac.....
Micro alternator 3kw
Voltage: 220V/380V - 24V/48V Hz : 50Hz Revolution : 500 Weight : 28kg Working efficiency.....
Micro alternator 10kw
Voltage: 220V/380V Ampere: 220V = 15A -- 380V = 26A Hz : 50Hz Revolution : 500 Weight : 48k.....
Solar Panel
we are interested in used/second hand or stock solar panels and other solar products. .....
Dawnice 100kwh 200kwh 300kwh 5...
About Dawnice

 How it Works
How it Works Pricing
Pricing FAQ
FAQ Quiz
Quiz Contact Us
Contact Us